Let's Make a Deal

I'm reading the book "Conversations on Game Theory" by Haim Shapira. There have been many books written on "Game Theory." I haven't read any of them, but I believe most of them talk a lot about formulas and equations. The book I'm reading is lots of fun and easy to read. It doesn't really talk much about formulas. In this book, Shapira brings up a lot of situations from everyday life among other situations. Tells you what would be the ideal thing to do (mathematically speaking), but then continues to say how things get complicated (and funny) when everyone follows the ideal behavior in these everyday life situations. I haven't finished the book just yet (just past halfway through), but if you can read Hebrew, I would recommend you get a copy.

One problem the book talks about is a well known one, at least by mathematicians, and that's the Monty Hall Problem. Some of you probably know it, but I'd like to share it anyways for those who haven't heard of it before.

It goes like this: You are a contestant on the game show "Let's Make a Deal." There are 3 doors behind one which there is a car. Behind each of the other two doors there is a goat. You pick one door, say door number 1. Now, the host, who knows what's behind each door, reveals one of the two other doors that you didn't choose, the door that has a goat. So now there are two doors left, the one that you choose at the beginning, and the one left unrevealed. One of them has a car, and the other has a goat.

The host now gives you a chance to switch doors, what do you do? Do you stay with door #1 your initial pick? Or do you switch to the other door left in the game? Remember, the host knows where the car is, maybe he is trying to make you switch to where the goat is so he can keep the car to himself (because his car was just stolen, and his wife might think he is cheating if he is late for supper...).

Well, there is a mathematical solutions to this question, which says that you should ALWAYS switch doors. And here is why:

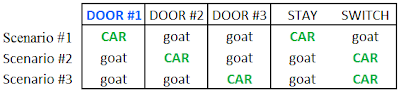
Scenario 1: car is behind door #1. You choose door #1, and switch, you lose.
Scenario 2: car is behind door #2. You choose door #1, and switch, you win.
Scenario 3: car is behind door #3. You choose door #1, and switch, you win.

You have 66.6 percent chance of winning the car if you switch. Confused? Maybe this will help:

Of course it gets tricky a little because on those types of game shows the host usually offers you money or other prizes to make you switch doors. (check out these videos if you're still confused: video 1, video 2).

Tomorrow morning I go in for a PET scan, and I believe a CT as well. I will probably have the results within a few hours, and then I'm seeing my doctor the following Monday where let's hope the news will be that I can take time off and that for now we are just going to wait and see. But I get the impression from my doctor that she expects more will need to be done. Either a surgery, or more, less drastic, chemo.

Huh, looks like I never updated here on the blog after I finished with my last round of chemo. I did mention it on Facebook. I guess I didn't have much to say or didn't feel like saying much, so I only updated on Facebook. You can Like the blog's page here.

So it's been two weeks since I finished the last (scheduled) chemo round. I've been feeling good over all. Though I feel like I might be coming down with a cold tomorrow. My throat is a bit dry and soar.
I emailed my doctor the other day to ask if I can eat raw food again. Food such as boiled egg, which I've been craving lately, and sushi and medium made steaks which I've been missing longly. Yesterday I had me some sushi, and today some steak for dessert!